Algebra 1 - solving Quadratic Equations

Solve the linear system: y = -2x + 9 and y = 3x - 4

1. Enter the first equation into Y₁.
2. Enter the second equation into Y₂.
3. Hit GRAPH.

4. Use the INTERSECT option to find where the two graphs intersect (the answer).
     2nd TRACE (CALC) #5 intersect
     Move spider close to the intersection.
     Hit ENTER 3 times.

5. Answer: x = 2.6 and y = 3.8

system

system2

system3

Comparing the graphical display with its Table.
To view the "table" that is formed when a graph is drawn, hit 2ndGraph (to get table). You can control what is displayed in the table by hitting 2nd Window (to get tblset)

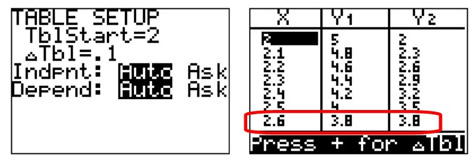
The images below show the table being set to start at 2, and the "delta"(Δ) Tbl set to .1, meaning the x-values will increase by .1 units as the x-values get larger.
The table shows that at an x-value of 2.6, the y-values in both equations will be 3.8. This is the intersection point (the system solution) for the two equations.

tablesystem3

Solve the linear system: x - 2y = 14 and x + 3y = 9

The graphing calculator will only accept entries that start with y = , so we need to solve these equations for
"y =".
system4

1. Enter the first equation into Y₁.
2. Enter the second equation into Y₂.
3. Hit GRAPH. The graphs appear to intersect OFF the window. We need MORE x-values to the right hand side of the graph. Go to WINDOW. Increase the size of Xmax. Hit GRAPH.

4. Use the INTERSECT option to find where the two graphs intersect (the answer).
     2nd TRACE (CALC) #5 intersect
     Move spider close to the intersection.
     Hit ENTER 3 times.

5. Answer: x = 12 and y = -1

system5

system6

Oops!!
They don't cross in the window. system7

Better!
Xmax was increased to 20. system8

Solve linear quadratic system: y = x² - 4x - 2 and y = x - 2

1. Enter the first equation into Y₁.
2. Enter the second equation into Y₂.
3. Hit GRAPH.

4. Use the INTERSECT option twice to find the two locations where the graphs intersect (the answers).
     2nd TRACE (CALC) #5 intersect
     Move spider close to the intersection.
     Hit ENTER 3 times.

5. Answer: (5,3) and (0,-2)

system9

system10

system11

system12