|
Matrices are rectangular
arrays of elements.
The dimension of a matrix is the number of
rows by the number of columns. |
|
|
Adding Matrices
- matrices must be of the same dimension to be added.
Add: 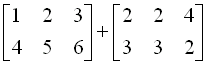
First Enter the Matrices (one at a time): |
|
Step 1: Go to Matrix
(above the x-1 key) 
If dimensions appear next to the names of the matrices,
such as 3x3, a matrix is already stored in the calculator. You
may save it by moving to a new name, or overwrite it.
|
Step 2: Arrow to the right to
EDIT
to allow for
entering the
matrix.
|
Step 3: Type in the dimensions (size) of your
matrix
and enter the elements (press ENTER).

|
|
Step 4: Repeat this process for
the second matrix
.  |
Step 5: Arrow to the right to
EDIT
and choose a
new name.
 |
Step 6: Type in the dimensions (size) of
your matrix
and enter the elements (press ENTER).
 |
|
Now, add:
Step 7: Return to the home
screen. Go to Matrix
to
get the names of the
matrices for adding.
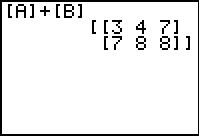 |
The answer to the addition, as seen
on the calculator screen,
is =
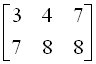 |
|
|
Multiplying Matrices- for multiplication to
occur, the dimensions of the matrices must be related in
the following manner: m x n times n x r
yields m x r
Multiply: 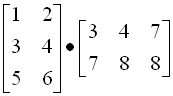
First Enter the Matrices (one at a time) as shown above: |
Step 1: Once the matrices are entered, you should
see their dimensions in residence when you go to Matrix
(above the x-1 key)
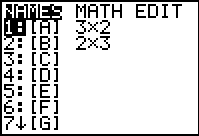
|
Step 2: Return to the home
screen. Go to Matrix
to
get the names of the
matrices for multiplying.
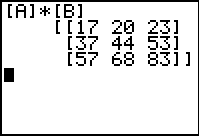 |
The product, as seen
on the calculator screen, is =
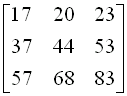
|
|
Using Matrices to Solve Systems of Equations:
1. (using the inverse coefficient matrix)
Write this system as a matrix equation and solve: 3x + 5y = 7 and 6x - y =
-8 |
|
Step 1: Line up the x, y and
constant values.
3x + 5y = 7
6x -
y = -8
|
Step 2: Write as equivalent
matrices.
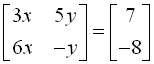 |
Step 3: Rewrite to separate out
the variables.
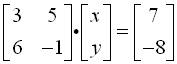 |
Step 4: Enter the two numerical matrices in the
calculator.
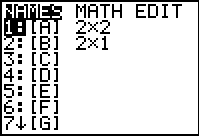 |
Step 5: The solution is obtained by multiplying both
sides of the equation by the inverse of the matrix which is multiplied
times
the variables.
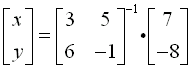 |
Step 6: Go to the home screen and enter the right side of
the previous equation.
 |
|
|
The answer to the system,
as seen on the calculator screen,
is x = -1 and y = 2.
|
Note: If the determinant of a matrix is zero, the matrix does not have an inverse. Thus, a single point, (x,y), solution cannot be found.
|