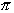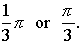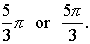|

Solving Trigonometric Equations
Remember: The calculator defaults
to Radian measure.
|
Problem: |
Find all values
of x for which
 |
|
|
Since this problem states the interval in terms of radians,
the answer will also need to be expressed in radians. |
Let's look at two possible solution
methods. The first method will work ONLY with Radians. The
second method will work with Degrees and then convert back to Radians
for the final answer. Pick the
method with which you feel most comfortable.
Method Using Only Radian: |
You are going to graph each side of the equation and look for all of
the points of intersection within the given interval.
|
Set the MODE to
Radian
 |
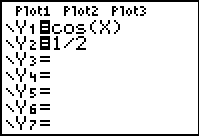
Set Y1 = left
side of equation.
Set Y2 = right side of equation.
 |
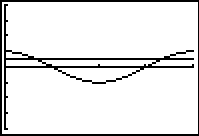
Start by hitting ZOOM #7
ZTrig.
Adjust WINDOW for
Xmin = 0 and Xmax = 2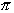
 |
|
Use the INTERSECT
option.
2nd TRACE (CALC) #5 intersect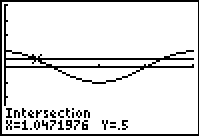 |
To express this answer in terms of
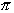 , ,
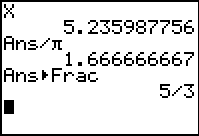
go to Home Screen and hit x ENTER.
Divide by
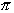 .
Convert to fraction. .
Convert to fraction.
MATH #1 ►Frac. ENTER.
 |
Answer:
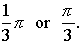 |
Now, find the second point of
intersection!
 |
Method Using Degree and Converting Back
to Radian: |
Again, you are going to graph each side of the equation and look for all of
the points of intersection within the given interval.
For this method, you must be aware that the interval in degrees is 0 < x < 360.
|
Set the MODE to
Degree
 |
Set Y1 = left
side of equation.
Set Y2 = right side of equation.
 |
Start by hitting ZOOM #7
ZTrig.
Adjust WINDOW for
Xmin = 0
and Xmax = 360
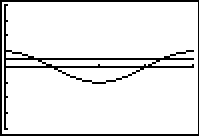 |
|
Use the INTERSECT
option.
2nd TRACE (CALC) #5 intersect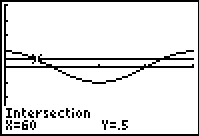 |
To convert to radians (in terms of
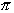 ), ),
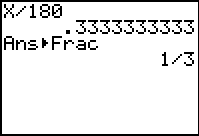
go to Home Screen and hit x/180 ENTER.
Convert to fraction.
MATH #1 ►Frac. ENTER.
 |
Answer:
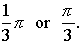 |
Now, find the second point of intersection!
 |
|
Use the INTERSECT
option again.
2nd TRACE (CALC) #5 intersect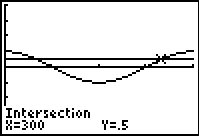 |
To convert to radians (in terms of
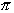 ), ),
go to Home Screen and hit x /180
ENTER.
Convert to fraction.
MATH #1 ►Frac. ENTER.
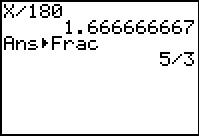 |
Answer:
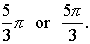 |
|

Finding Your Way Around
TABLE of CONTENTS
|