|
While the basic TI-84+ calculator will not list the factors of an expression, you can still use the calculator to help in factoring algebraic expressions. There are several approaches you may use
depending upon the known information.
Answers can be
"checked" to see if the
correct factors have been found:
(particularly helpful when dealing with multiple choice
questions)
Check Method 1: Check factors/answer on the home
screen in equation form.
Factor x2 - 12x + 36.
OR Find (x - 6)2.
|
- Choose your "favorite" positive
one-digit (for ease) integer value and store the
value in x (do not pick 0 or 1).
For example, to store a 7: 7 STO► x
- Hit ENTER.
- Enter the problem to be factored (or
multiplied) and set "=" to one of the
possible answers (or the answer you want to
check).
The "=" sign is under
2nd MATH (TEST) #1 =.
- Hit ENTER.
- If a 0
appears, this is NOT the correct answer.
If a 1 appears, this IS
the correct answer.
|

Remember that (x - 6)2
is the same as
(x - 6)(x - 6). |
For this problem, we now know that x2 - 12x + 36 = (x - 6)(x - 6).
We also know that (x - 6)2 = x2 - 12x + 36, and NOT x2 + 36 nor x2 - 36. |
|
Check Method 2: Check factors/answer by graphing.
Factor x2 - 12x + 36.
OR Find (x - 6)2.
|
- Enter the expression into the
Y1= on the
calculator.
- Enter the possible answer response into
Y2=.
- Move to the left of the
Y2= and choose
the open circle. This setting will allow
you to clearly see the animated circle
crossing the screen.
- When the answer is correct, the animated
circle will be "riding" on top of the
original graph.
- Keep checking until the correct answer
is found.
- The only difficult feature of this
method is the occasional need to adjust the
viewing window to see the graph.
|
|
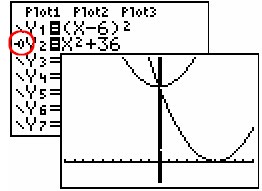
The animated bubble does not run along the
original curve. It forms its own graph.
This is not the correct solution.
|
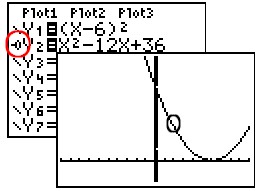
The animated bubble runs along the
original graph. This is the answer. |
Again, we see that (x - 6)2 = x2 - 12x + 36, and NOT x2 + 36.
This also verifies that x2 - 12x + 36 = (x - 6)(x - 6). |
|
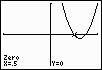
Answers can be "found"
by graphing and finding the zeros of an equation.
Graph Method:
Factors can be found by finding the
zeros of an equation.
Find the factors of x2 - 3x -
4.
|
|
Example 1:
(Multiple choice question)
The factors of x2 + 5x +6 are
(1) (x + 1)(x + 6)
(2) (x + 3)(x + 2)
(3) (x + 5)(x + 1)
(4) (x + 6)(x - 1)
|
Method 1:
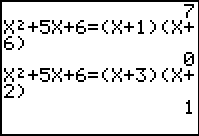
The "favorite" number stored was 7.
When you hit ENTER and a "1" appears,
you have found the
answer. |
|
Method
2:
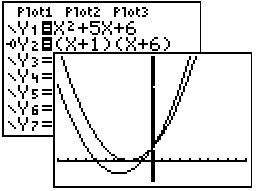
The two graphs do not overlap.
This is not the answer.
|
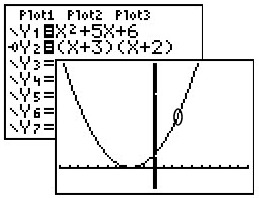
The animated bubble overlaps the
original graph. This is the answer.
|
Example 2:
(Multiple choice question)
The room that is shown in the figure below has a floor space
of 2x2 + x - 15
square feet. If the width of the room is (x + 3) feet,
what is the length?

(1) (x - 3)
(2) (2x - 5)
(3) (x - 5)
(4) (2x + 5) |
Method 1:

Answers are tested until the correct
answer is found.
OR
Check your answer to be sure
you chose wisely. |
Method 2:
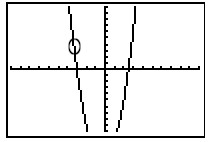 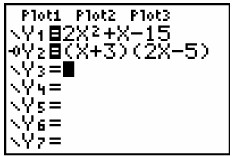
|



![]()